Skip to content

MindDiffuser-Controlled Image Reconstruction from Human Brain Activity with Semantic and Structural Diffusion

🔥INFO

Blog: 2025/07/21 by IgniSavium

  • Title: MindDiffuser-Controlled Image Reconstruction from Human Brain Activity with Semantic and Structural Diffusion
  • Authors: Yizhuo Lu, Huiguang He et al. (CAS)
  • Published: March 2023
  • Comment: ACM Multimedia
  • URL: https://arxiv.org/abs/2303.14139

🥜TLDR: Preserve structural information in fMRI-to-image reconstruction by iteratively backpropagating Stable Diffusion inputs guided by CLIP low-layer feature supervision.

Motivation

The research aims to address the challenge of reconstructing visual stimuli from fMRI data by developing a two-stage model (based on Stable Diffusion) that simultaneously ensures semantic richness and structural alignment, overcoming limitations in previous methods that either lacked clear semantic details or controlled structural features like position and orientation.

image-20250721162648316

Model

Architecture

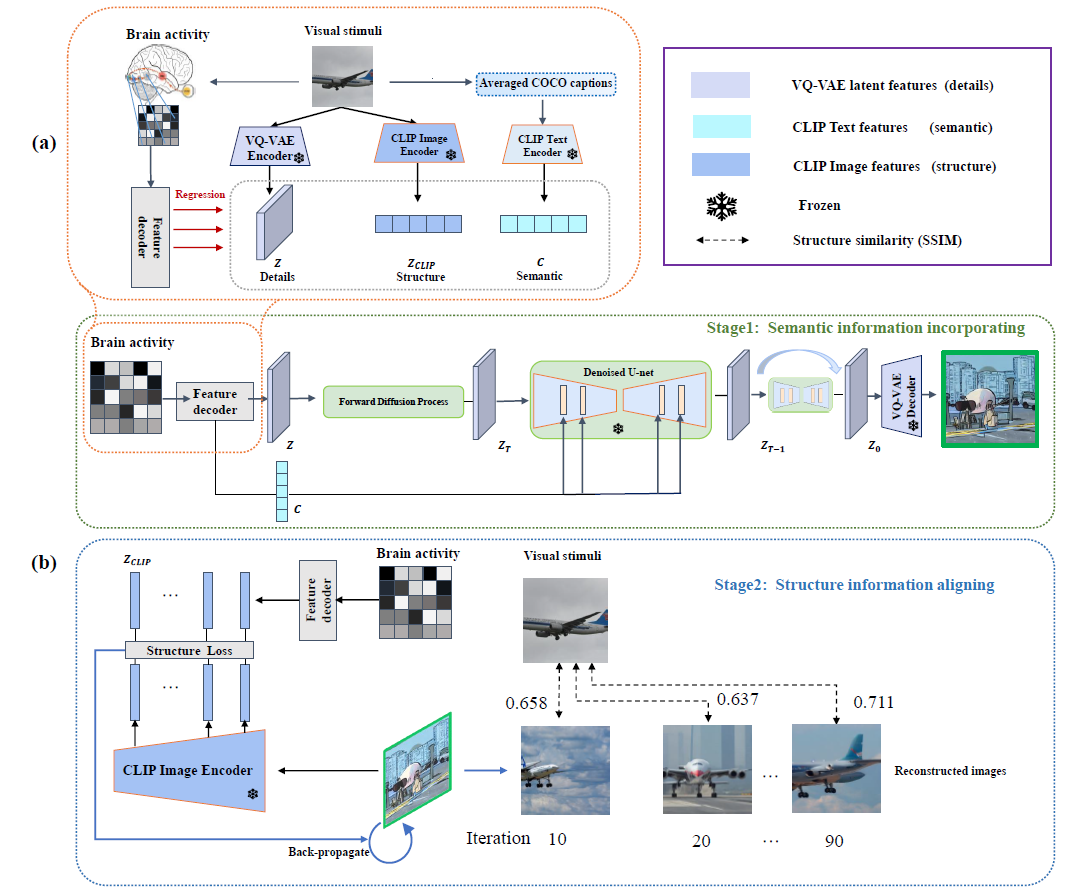
image-20250721161717752

Stage-1: linear transform fMRI into original visual latent state \(z\) and text condition \(c\) in Stable Diffusion img2img process.

Stage-2: iteratively backpropagate \(z,c\) to align the lower CLIP layer features (which contains structural information such as position and orientation) between generated images and original images (extracted via trained linear transformation from fMRI)

Evaluation

image-20250721164807727

Performance

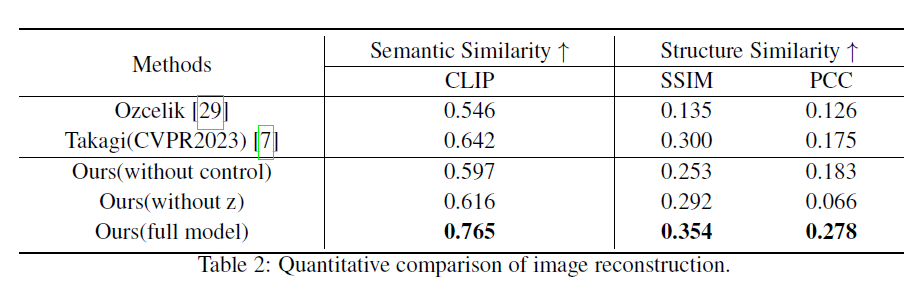
  • CLIP last layer cosine similarity for semantic comparison

SSIM (Structural Similarity Index Measure)

  • From -1 to 1, but typically between 0 and 1;
  • 1 indicates that the two images are structurally identical.
\[ SSIM(x,y)=\frac{(2\mu_x\mu_y + C_1)(2\sigma_{xy} + C_2)}{(\mu_x^2 + \mu_y^2 + C_1)(\sigma_x^2 + \sigma_y^2 + C_2)} \]

Where:

  • \(\mu_x, \mu_y\): The mean values (brightness) of images \(x\) and \(y\);
  • \(\sigma_x^2, \sigma_y^2\): Variance (contrast);
  • \(\sigma_{xy}\): Covariance (structural similarity);
  • \(C_1, C_2\): Stabilizing constants to prevent division by zero.

Per-pixel correlation coefficient (Pixel-wise Correlation Coefficient)

  • From -1 to 1;
  • 1 indicates perfect positive correlation (every pixel matches);
  • 0 indicates no correlation;
  • -1 indicates perfect negative correlation.

Assuming the two images are flattened into two vectors \(x\) and \(y\), the correlation coefficient is: $$ r= \frac{\sum (x_i - \bar{x})(y_i - \bar{y})}{\sqrt{\sum (x_i - \bar{x})^2 \sum (y_i - \bar{y})^2}} $$ Where:

  • \(\bar{x}, \bar{y}\) are the mean pixel values of the two images;
  • This is essentially the Pearson correlation coefficient from statistics, applied to the pixel arrays of the images.

image-20250721164840191

image-20250721164900477

Cross-subject adaptability

image-20250721165720578

Criticality of guided origin latent \(z\)

image-20250721165951145